how to find square root of decimal number

To find the square root of numbers in the decimal form are explained in the following steps:

Step I: Make the number of decimal places even by affixing a zero on the extreme right of the decimal part (if required).

Step II: In the integral part, mark the periods as done while finding the square root of a perfect square of some natural number.

Step III: In the decimal part, mark the periods on every pair of digits beginning with the first decimal place.

Step IV: Now, find the square root by long division method.

Step V: Put the decimal point in the square root as soon as the integral part is exhausted.

Examples on square root of numbers in decimal form:

1. Evaluate: √42.25

Solution:

Using the division method we may find the square root of the given number;

Therefore, √42.25 = 6.5

2. Evaluate: √1.96

Solution:

Using the division method we may find the square root of the given number;

Therefore, √1.96 = 1.4

3. Evaluate: √6.4009

Solution:

Using the division method we may find the square root of the given number;

Therefore, √6.4009 = 2.53

4. Evaluate: √66.4225

Solution: 

Using the division method we may find the square root of the given number;

Therefore, √66.4225 = 8.15

5. Evaluate: √0.4225

Solution:

Using the division method we may find the square root of the given number;

Therefore, √0.4225 = 0.65

square of a number easy trick math ssc bank po railway exam

square root

(algorithm)

Definition: This describes a “long hand” or manual method of calculating or extracting square roots. Calculation of a square root by hand is a little like long-hand division.

Suppose you need to find the square root of 66564. Set up a “division” with the number under the radical. Mark off pairs of digits, starting from the decimal point and working left. (Here the decimal point is a period (.) and commas (,) mark pairs of digits.)

               ___________	
             \/  6,65,64.	

Look at the leftmost digit(s) (6 in this case). What is the largest number whose square is less than or equal to it? It is 2, whose square is 4. Write 2 above, write the square below and subtract.

               __2________	
             \/  6,65,64.	
                -4		
               ----		
                 2		

Now bring down the next two digits (65). The next “divisor” is double the number on top (2×2=4) and some other digit in the units position (4_).

               __2________	
             \/  6,65,64.	
                -4		
                -----		
             4_ ) 265		

What is the largest number that we can put in the units and also multiply times the divisor such that the result is still be less than or equal to what we have? (Algebraically, what is d such that d × (40+d) ≤ 265?) It looks like 6 might work (since 6 × 40 = 240), but 6 is too big, since 6 × 46 = 276:

               __2__6_____	
             \/  6,65,64.	
                -4		
                -----		
             46 ) 265		
                 -276   TOO BIG	

So try 5 instead.

               __2__5_____	
             \/  6,65,64.	
                -4		
                -----		
             45 ) 265		
                 -225		
                 -------		
                   40		

Repeat: bring down the next two digits, and double the number on top (2 × 25 = 50) to make a “divisor”, with another unit.

               __2__5_____	
             \/  6,65,64.	
                -4		
                -----		
             45 ) 265		
                 -225		
                 -------		
             50_ ) 4064		

It looks like 8 would work. Let’s see.

               __2__5__8__	
             \/  6,65,64.	
                -4		
                -----		
             45 ) 265		
                 -225		
                 -------		
             508 ) 4064		
                  -4064		
                  ------		
                      0		

So the square root of 66564 is 258. You can continue for as many decimal places as you need: just bring down more pairs of zeros.

Here is an example spanning the decimal point. When a number does not have a rational square root, you can continue calculating (significant) digits as long as you wish.

       __1__6.8_4_0_4_2_7_5_...
     \/  2,83.6		
        -1		
        -----		
     26 ) 183		
         -156		
         ------		
     328 ) 2760		
          -2624		
          -------	
     3364 ) 13600	
           -13456	
           --------	
     33680 )  14400	
                 -0	
            ---------	
     336804 ) 1440000	
             -1347216	
             ----------	
     3368082 )  9278400	
               -6736164	
              -----------	
     33680847 ) 254223600	
               -235765929	
               ------------	
     336808545 ) 1845767100	
                -1684042725	
                -----------	
                  161724375	

Why does this work?

Consider (10A + B)² = 100A² + 2 × 10AB + B² and think about finding the area of a square. Remember that 10A + B is just the numeral with B in the units place and A in the higher position. For 42, A=4 and B=2, so 10 × 4 + 2 = 42.

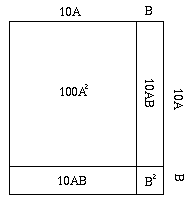
The area of the two skinny rectangles is 2 × 10A × B. The tiny square is B². If we know A and the area of the square, S, what B should we choose?

We previously subtracted A² from S. To scale to 100A², we bring down two more digits (a factor of 100) of the size of S. We write down twice A (2A), but shifted one place to leave room for B (10 × 2A or 2 × 10A). Now we add B to get 2 × 10A + B. Multiplying by B gives us 2 × 10AB + B². When we subtract that from the remainder (remember we already subtracted A²), we have subtracted exactly (10A + B)². That is, we have improved our knowledge of the square root by one digit, B.

We take whatever remains, scale again by 100, by bringing down two more digits, and repeat the process.

See also cube root.

Note: In computers and hand-held calculators, square root, sine, cosine, and other transcendental functions are calculated with sophisticated functions, such as Taylor series, CORDIC, or Newton-Raphson method, sometimes called Newton’s method. This lesson explains, for instance, possible difficulties in convergence.

Author: PEB

Implementation

GAMS Class C2 has many implementations of powers, roots, and reciprocals (C and Fortran). Many variations (C and Assembler) for caching, pipelined processing, etc.

More information

Another geometric justification.

---

Go to the Dictionary of Algorithms and Data Structures home page.

---

If you have suggestions, corrections, or comments, please get in touch with Paul Black.

Entry modified 8 September 2014.
HTML page formatted Mon Dec 12 09:26:39 2016.

Cite this as:
Paul E. Black, “square root”, in Dictionary of Algorithms and Data Structures [online], Vreda Pieterse and Paul E. Black, eds. 8 September 2014. (accessed TODAY) Available from: https://www.nist.gov/dads/HTML/squareRoot.html

How to find square of a number

and should your child learn how to do it

Most people in today’s world feel that since calculators can find square roots, that children don’t need to learn how to find square roots using any pencil-and-paper method. However, learning at least the “guess and check” method for finding the square root will actually help the students UNDERSTAND and remember the square root concept itself!

So even though your math book may totally dismiss the topic of finding square roots without a calculator, consider letting students learn and practice at least the “guess and check” method. Since it actually deals with the CONCEPT of square root, I would consider it as essential for students to learn.

Depending on the situation and the students, the “guess and check” method can either be performed with a simple calculator that doesn’t have a square root button or with paper & pencil calculations.

 

Finding square roots by guess & check method

To find a decimal approximation to, say √2, first make an initial guess, then square the guess, and depending how close you got, improve your guess. Since this method involves squaring the guess (multiplying the number times itself), it uses the actual definition of square root, and so can be very helpful in teaching the concept of square root.

 

Example: what is square root of 20?

You can start out by noting that since √16 = 4 and √25 = 5, then √20 must be between 4 and 5.

Then make a guess for √20; let’s say for example that it is 4.5. Square that, see if the result is over or under 20, and improve your guess based on that. Repeat this process until you have the desired accuracy (amount of decimals). It’s that simple and can be a nice experiment for students!

 

Example: Find √6 to 4 decimal places

Since 2² = 4 and 3² = 9, we know that √6 is between 2 and 3. Let’s guess (or estimate) that it is 2.5. Squaring that we get 2.5² = 6.25. That’s too high, so we reduce our estimate a little. Let’s try 2.4 next. To find the square root of 6 to four decimal places we need to repeat this process until we have five decimals, and then we will round the result.

Estimate	Square of estimate	High/low
2.4	5.76	Too low
2.45	6.0025	Too high but real close
2.449	5.997601	Too low
2.4495	6.00005025	Too high so the square root of 6 must be between 2.449 and 2.4495.
2.4493	5.99907049	Too low
2.4494	5.99956036	Too low, so the square root of 6 must be between 2.4494 and 2.4495
2.44945	5.9998053025	Too low, so the square root of 6 must be between 2.44945 and 2.4495.

This is enough iterations since we know now that √6 would be rounded to 2.4495 (and not to 2.4494).

 

Finding square roots using an algorithm

There is also an algorithm for square roots that resembles the long division algorithm, and it was taught in schools in days before calculators. See the example below to learn it. While learning this algorithm may not be necessary in today’s world with calculators, working out some examples can be used as an exercise in basic operations for middle school students, and studying the logic behind it can be a good thinking exercise for high school students.

 

Example: Find √645 to one decimal place.

First group the numbers under the root in pairs from right to left, leaving either one or two digits on the left (6 in this case). For each pair of numbers you will get one digit in the square root.

To start, find a number whose square is less than or equal to the first pair or first number, and write it above the square root line (2):

2
√6	.45

Then continue this way:

2 √6 .45  – 4 2 45	2 √6 .45  – 4 (4 _) 2 45	2 √6 .45  – 4 (45) 2 45
Square the 2, giving 4, write that underneath the 6, and subtract. Bring down the next pair of digits.	Then double the number above the square root symbol line (highlighted), and write it down in parenthesis with an empty line next to it as shown.	Next think what single-digit number something could go on the empty line so that forty-something times something would be less than or equal to 245. 45 x 5 = 225 46 x 6 = 276, so 5 works.
2 5 √6 .45 .00  – 4 (45) 2 45 – 2 25 20 00	2 5 √6 .45 .00  – 4 (45) 2 45 – 2 25 (50_) 20 00	2 5 . 3 √6 .45 .00  – 4 (45) 2 45 – 2 25 (503) 20 00
Write 5 on top of line. Calculate 5 x 45, write that below 245, subtract, bring down the next pair of digits (in this case the decimal digits 00).	Then double the number above the line (25), and write the doubled number (50) in parenthesis with an empty line next to it as indicated:	Think what single digit number something could go on the empty line so that five hundred-something times something would be less than or equal to 2000. 503 x 3 = 1509 504 x 4 = 2016, so 3 works.
2 5 . 3 √6 .45 .00 .00  – 4 (45) 2 45 – 2 25 (503) 20 00 –  15 09 4 91 00	2 5 . 3 √6 .45 .00 .00  – 4 (45) 2 45 – 2 25 (503) 20 00 –  15 09 (506_) 4 91 00	2 5 . 3 9 √6 .45 .00 .00  – 4 (45) 2 45 – 2 25 (503) 20 00 –  15 09 (506_) 4 91 00
Calculate 3 x 503, write that below 2000, subtract, bring down the next digits.	Then double the ‘number’ 253 which is above the line (ignoring the decimal point), and write the doubled number 506 in parenthesis with an empty line next to it as indicated:	5068 x 8 = 40544 5069 x 9 = 45621, which is less than 49100, so 9 works.

Thus to one decimal place, √645 = 25.4